12月 10, 2018 —
Posted by Mike Shwe, Product Manager for TensorFlow Probability at Google; Josh Dillon, Software Engineer for TensorFlow Probability at Google; Bryan Seybold, Software Engineer at Google; Matthew McAteer; and Cam Davidson-Pilon.
New to probabilistic programming? New to TensorFlow Probability (TFP)? Then we’ve got something for you. Bayesian Methods for Hackers, an introductory, hands-on tutorial,…
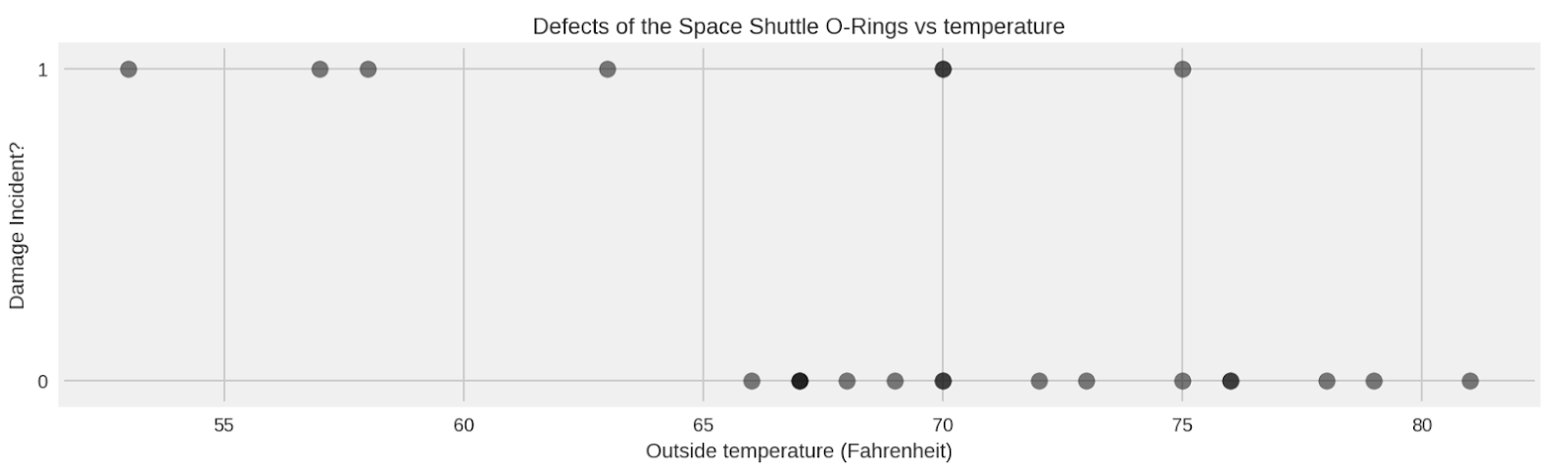

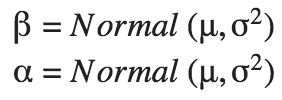
tfp.distributions.Normal, as in this code snippet:temperature_ = challenger_data_[:, 0]
temperature = tf.convert_to_tensor(temperature_, dtype=tf.float32)
D_ = challenger_data_[:, 1] # defect or not?
D = tf.convert_to_tensor(D_, dtype=tf.float32)
beta = tfd.Normal(name="beta", loc=0.3, scale=1000.).sample()
alpha = tfd.Normal(name="alpha", loc=-15., scale=1000.).sample()
p_deterministic = tfd.Deterministic(name="p", loc=1.0/(1. + tf.exp(beta * temperature_ + alpha))).sample()
[
prior_alpha_,
prior_beta_,
p_deterministic_,
D_,
] = evaluate([
alpha,
beta,
p_deterministic,
D,
])evaluate() helper function allows us to transition between graph and eager modes seamlessly, while converting tensor values to numpy. We describe eager and graph modes, as well as this helper function in more detail in the beginning of Chapter 2.
joint_log_prob are data and model state. The function returns the log of the joint probability that the parameterized model generated the observed data. To learn more about the joint_log_prob, please see this vignette.joint_log_prob:def challenger_joint_log_prob(D, temperature_, alpha, beta):
"""
Joint log probability optimization function.
Args:
D: The Data from the challenger disaster representing presence or
absence of defect
temperature_: The Data from the challenger disaster, specifically the temperature on
the days of the observation of the presence or absence of a defect
alpha: one of the inputs of the HMC
beta: one of the inputs of the HMC
Returns:
Joint log probability optimization function.
"""
rv_alpha = tfd.Normal(loc=0., scale=1000.)
rv_beta = tfd.Normal(loc=0., scale=1000.)
logistic_p = 1.0/(1. + tf.exp(beta * tf.to_float(temperature_) + alpha))
rv_observed = tfd.Bernoulli(probs=logistic_p)
return (
rv_alpha.log_prob(alpha)
+ rv_beta.log_prob(beta)
+ tf.reduce_sum(rv_observed.log_prob(D))
)rv_alpha and rv_beta represent the random variables for our prior distributions for 𝛼 and β. By contrast, rv_observedrepresents the conditional distribution for the likelihood of observations in temperature and O-ring outcome, given a logistic distribution parameterized by 𝛼 and β.joint_log_prob function, and send it to the tfp.mcmc module. Markov chain Monte Carlo (MCMC) algorithms make educated guesses about the unknown input values, computing the likelihood of the set of arguments in the joint_log_prob function. By repeating this process many times, MCMC builds a distribution of likely parameters. Constructing this distribution is the goal of probabilistic inference.challenge_joint_log_prob function:number_of_steps = 10000
burnin = 2000
# Set the chain's start state.
initial_chain_state = [
0. * tf.ones([], dtype=tf.float32, name="init_alpha"),
0. * tf.ones([], dtype=tf.float32, name="init_beta")
]
# Since HMC operates over unconstrained space, we need to transform the
# samples so they live in real-space.
# Alpha is 100x of beta approximately, so apply Affine scalar bijector
# to multiply the unconstrained alpha by 100 to get back to
# the Challenger problem space
unconstraining_bijectors = [
tfp.bijectors.AffineScalar(100.),
tfp.bijectors.Identity()
]
# Define a closure over our joint_log_prob.
unnormalized_posterior_log_prob = lambda *args: challenger_joint_log_prob(D, temperature_, *args)
# Initialize the step_size. (It will be automatically adapted.)
with tf.variable_scope(tf.get_variable_scope(), reuse=tf.AUTO_REUSE):
step_size = tf.get_variable(
name='step_size',
initializer=tf.constant(0.5, dtype=tf.float32),
trainable=False,
use_resource=True
)
# Defining the HMC
hmc=tfp.mcmc.TransformedTransitionKernel(
inner_kernel=tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=unnormalized_posterior_log_prob,
num_leapfrog_steps=40, #to improve convergence
step_size=step_size,
step_size_update_fn=tfp.mcmc.make_simple_step_size_update_policy(
num_adaptation_steps=int(burnin * 0.8)),
state_gradients_are_stopped=True),
bijector=unconstraining_bijectors)
# Sampling from the chain.
[
posterior_alpha,
posterior_beta
], kernel_results = tfp.mcmc.sample_chain(
num_results = number_of_steps,
num_burnin_steps = burnin,
current_state=initial_chain_state,
kernel=hmc)
# Initialize any created variables for preconditions
init_g = tf.global_variables_initializer()evaluate() helper function:evaluate(init_g)
[
posterior_alpha_,
posterior_beta_,
kernel_results_
] = evaluate([
posterior_alpha,
posterior_beta,
kernel_results
])
print("acceptance rate: {}".format(
kernel_results_.inner_results.is_accepted.mean()))
print("final step size: {}".format(
kernel_results_.inner_results.extra.step_size_assign[-100:].mean()))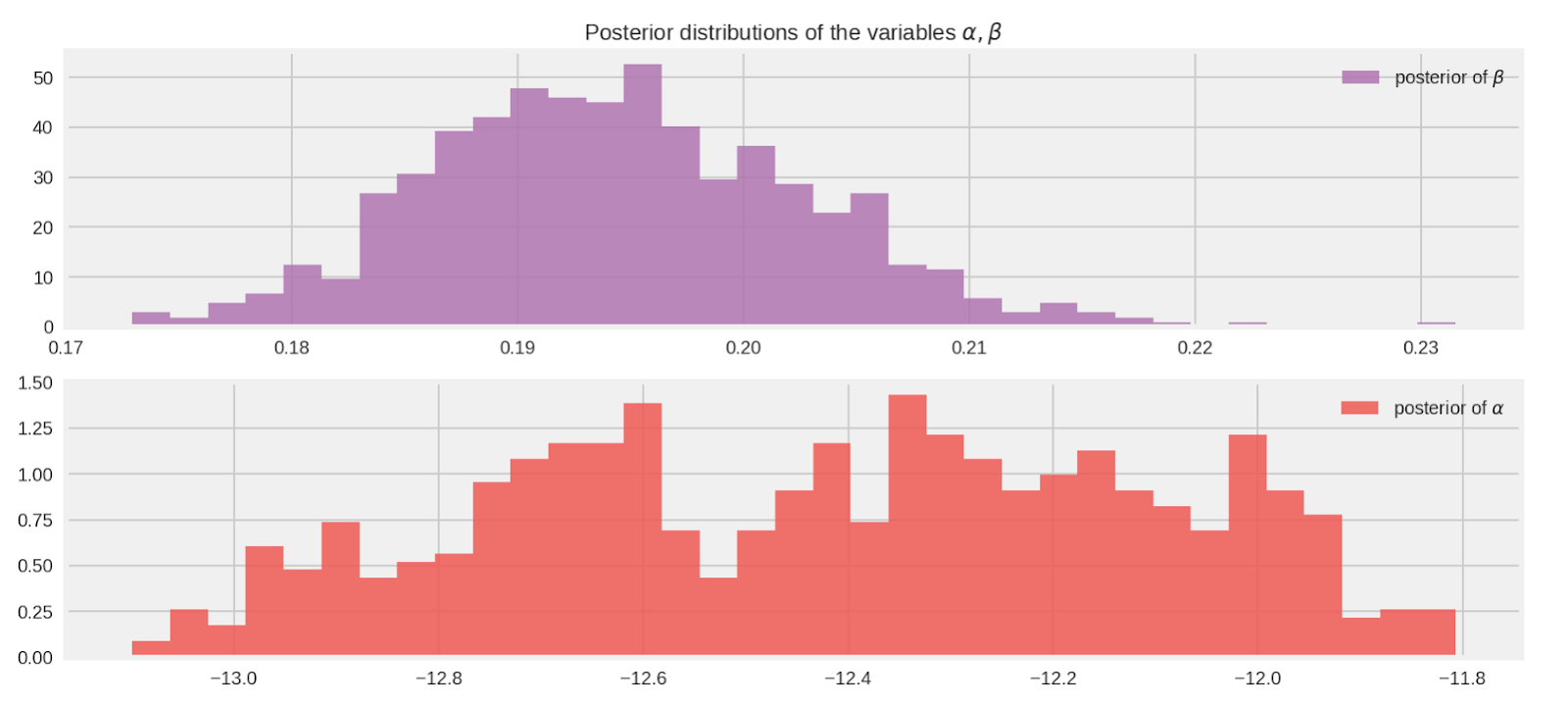
alpha_samples_1d_ = posterior_alpha_[:, None] # best to make them 1d
beta_samples_1d_ = posterior_beta_[:, None]
beta_mean = tf.reduce_mean(beta_samples_1d_.T[0])
alpha_mean = tf.reduce_mean(alpha_samples_1d_.T[0])
[ beta_mean_, alpha_mean_ ] = evaluate([ beta_mean, alpha_mean ])
print("beta mean:", beta_mean_)
print("alpha mean:", alpha_mean_)
def logistic(x, beta, alpha=0):
"""
Logistic function with alpha and beta.
Args:
x: independent variable
beta: beta term
alpha: alpha term
Returns:
Logistic function
"""
return 1.0 / (1.0 + tf.exp((beta * x) + alpha))
t_ = np.linspace(temperature_.min() - 5, temperature_.max() + 5, 2500)[:, None]
p_t = logistic(t_.T, beta_samples_1d_, alpha_samples_1d_)
mean_prob_t = logistic(t_.T, beta_mean_, alpha_mean_)
[
p_t_, mean_prob_t_
] = evaluate([
p_t, mean_prob_t
])



12月 10, 2018
—
Posted by Mike Shwe, Product Manager for TensorFlow Probability at Google; Josh Dillon, Software Engineer for TensorFlow Probability at Google; Bryan Seybold, Software Engineer at Google; Matthew McAteer; and Cam Davidson-Pilon.
New to probabilistic programming? New to TensorFlow Probability (TFP)? Then we’ve got something for you. Bayesian Methods for Hackers, an introductory, hands-on tutorial,…