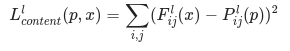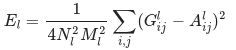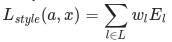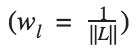Posted by Raymond Yuan, Software Engineering Intern

In this tutorial, we will learn how to use deep learning to compose images in the style of another image (ever wish you could paint like Picasso or Van Gogh?). This is known as neural style transfer! This is a technique outlined in Leon A. Gatys’ paper, A Neural Algorithm of Artistic Style, which is a great read, and you should definitely check it out.

Neural style transfer is an optimization technique used to take three images, a content image, a style reference image (such as an artwork by a famous painter), and the input image you want to style — and blend them together such that the input image is transformed to look like the content image, but “painted” in the style of the style image.

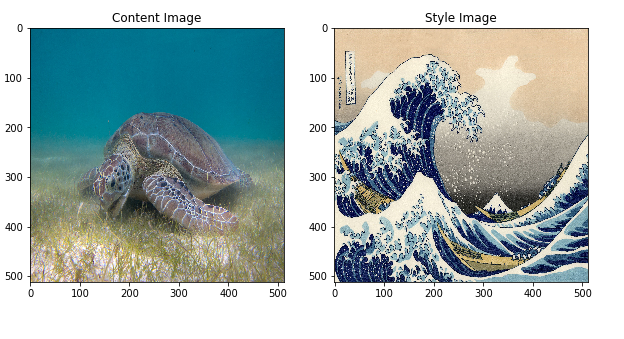
For example, let’s take an image of this turtle and Katsushika Hokusai’s The Great Wave off Kanagawa:

Image of Green Sea Turtle by P. Lindgren, from Wikimedia Commons

Now how would it look like if Hokusai decided to add the texture or style of his waves to the image of the turtle? Something like this?

Is this magic or just deep learning? Fortunately, this doesn’t involve any magic: style transfer is a fun and interesting technique that showcases the capabilities and internal representations of neural networks.

The principle of neural style transfer is to define two distance functions, one that describes how different the content of two images are, Lcontent, and one that describes the difference between the two images in terms of their style, Lstyle. Then, given three images, a desired style image, a desired content image, and the input image (initialized with the content image), we try to transform the input image to minimize the content distance with the content image and its style distance with the style image.

In summary, we’ll take the base input image, a content image that we want to match, and the style image that we want to match. We’ll transform the base input image by minimizing the content and style distances (losses) with backpropagation, creating an image that matches the content of the content image and the style of the style image.

Specific concepts that will be covered:

In the process, we will build practical experience and develop intuition around the following concepts:

• Eager Execution — use TensorFlow’s imperative programming environment that evaluates operations immediately
  
• Learn more about eager execution
  
• See it in action (many of the tutorials are runnable in Colaboratory)
  
• Using Functional API to define a model — we’ll build a subset of our model that will give us access to the necessary intermediate activations using the Functional API
  
• Leveraging feature maps of a pretrained model — Learn how to use pretrained models and their feature maps
  
• Create custom training loops — we’ll examine how to set up an optimizer to minimize a given loss with respect to input parameters
  

We will follow the general steps to perform style transfer:

1. Visualize data
   
2. Basic Preprocessing/preparing our data
   
3. Set up loss functions
   
4. Create model
   
5. Optimize for loss function

Audience: This post is geared towards intermediate users who are comfortable with basic machine learning concepts. To get the most out of this post, you should:

• Read Gatys’ paper — we’ll explain along the way, but the paper will provide a more thorough understanding of the task
  
• Understand gradient descent
  

Time Estimated: 60 min

Code:

You can find the complete code for this article at this link. If you’d like to step through this example, you can find the colab here.

Implementation

We’ll begin by enabling eager execution. Eager execution allows us to work through this technique in the clearest and most readable way.

tf.enable_eager_execution()
print("Eager execution: {}".format(tf.executing_eagerly()))
 
Here are the content and style images we will use: 
plt.figure(figsize=(10,10))

content = load_img(content_path).astype('uint8')
style = load_img(style_path)

plt.subplot(1, 2, 1)
imshow(content, 'Content Image')

plt.subplot(1, 2, 2)
imshow(style, 'Style Image')
plt.show()

Image of Green Sea Turtle -By P .Lindgren from Wikimedia Commons and Image of The Great Wave Off Kanagawa from by Katsushika Hokusai Public Domain

Define content and style representations

In order to get both the content and style representations of our image, we will look at some intermediate layers within our model. Intermediate layers represent feature maps that become increasingly higher ordered as you go deeper. In this case, we are using the network architecture VGG19, a pretrained image classification network. These intermediate layers are necessary to define the representation of content and style from our images. For an input image, we will try to match the corresponding style and content target representations at these intermediate layers.

Why intermediate layers?

You may be wondering why these intermediate outputs within our pretrained image classification network allow us to define style and content representations. At a high level, this phenomenon can be explained by the fact that in order for a network to perform image classification (which our network has been trained to do), it must understand the image. This involves taking the raw image as input pixels and building an internal representation through transformations that turn the raw image pixels into a complex understanding of the features present within the image. This is also partly why convolutional neural networks are able to generalize well: they’re able to capture the invariances and defining features within classes (e.g., cats vs. dogs) that are agnostic to background noise and other nuisances. Thus, somewhere between where the raw image is fed in and the classification label is output, the model serves as a complex feature extractor; hence by accessing intermediate layers, we’re able to describe the content and style of input images.

Specifically we’ll pull out these intermediate layers from our network:

# Content layer where will pull our feature maps
content_layers = ['block5_conv2'] 

# Style layer we are interested in
style_layers = ['block1_conv1',
                'block2_conv1',
                'block3_conv1', 
                'block4_conv1', 
   'block5_conv1'
               ]

num_content_layers = len(content_layers)
num_style_layers = len(style_layers)

Model

In this case, we load VGG19, and feed in our input tensor to the model. This will allow us to extract the feature maps (and subsequently the content and style representations) of the content, style, and generated images.

We use VGG19, as suggested in the paper. In addition, since VGG19 is a relatively simple model (compared with ResNet, Inception, etc) the feature maps actually work better for style transfer.

In order to access the intermediate layers corresponding to our style and content feature maps, we get the corresponding outputs by using the Keras Functional API to define our model with the desired output activations.

With the Functional API, defining a model simply involves defining the input and output: model = Model(inputs, outputs).

def get_model():
  """ Creates our model with access to intermediate layers. 
  
  This function will load the VGG19 model and access the intermediate layers. 
  These layers will then be used to create a new model that will take input image
  and return the outputs from these intermediate layers from the VGG model. 
  
  Returns:
    returns a keras model that takes image inputs and outputs the style and 
      content intermediate layers. 
  """
  # Load our model. We load pretrained VGG, trained on imagenet data (weights=’imagenet’)
  vgg = tf.keras.applications.vgg19.VGG19(include_top=False, weights='imagenet')
  vgg.trainable = False
  # Get output layers corresponding to style and content layers 
  style_outputs = [vgg.get_layer(name).output for name in style_layers]
  content_outputs = [vgg.get_layer(name).output for name in content_layers]
  model_outputs = style_outputs + content_outputs
  # Build model 
  return models.Model(vgg.input, model_outputs)

In the above code snippet, we’ll load our pretrained image classification network. Then we grab the layers of interest as we defined earlier. Then we define a Model by setting the model’s inputs to an image and the outputs to the outputs of the style and content layers. In other words, we created a model that will take an input image and output the content and style intermediate layers!

Define and create our loss functions (content and style distances)

Content Loss:

Our content loss definition is actually quite simple. We’ll pass the network both the desired content image and our base input image. This will return the intermediate layer outputs (from the layers defined above) from our model. Then we simply take the euclidean distance between the two intermediate representations of those images. More formally, content loss is a function that describes the distance of content from our input image x and our content image, p . Let Cₙₙ be a pre-trained deep convolutional neural network. Again, in this case we use VGG19. Let X be any image, then Cₙₙ(x) is the network fed by X. Let Fˡᵢⱼ(x)∈ Cₙₙ(x)and Pˡᵢⱼ(x) ∈ Cₙₙ(x) describe the respective intermediate feature representation of the network with inputs x and p at layer l . Then we describe the content distance (loss) formally as: We perform backpropagation in the usual way such that we minimize this content loss. We thus change the initial image until it generates a similar response in a certain layer (defined in content_layer) as the original content image.

This can be implemented quite simply. Again it will take as input the feature maps at a layer L in a network fed by x, our input image, and p, our content image, and return the content distance.

def get_content_loss(base_content, target):
  return tf.reduce_mean(tf.square(base_content - target))

Style Loss:

Computing style loss is a bit more involved, but follows the same principle, this time feeding our network the base input image and the style image. However, instead of comparing the raw intermediate outputs of the base input image and the style image, we instead compare the Gram matrices of the two outputs.

Mathematically, we describe the style loss of the base input image, x, and the style image, a, as the distance between the style representation (the gram matrices) of these images. We describe the style representation of an image as the correlation between different filter responses given by the Gram matrix Gˡ, where Gˡᵢⱼ is the inner product between the vectorized feature map i and j in layer l. We can see that Gˡᵢⱼ generated over the feature map for a given image represents the correlation between feature maps i and j.

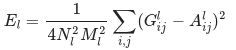
To generate a style for our base input image, we perform gradient descent from the content image to transform it into an image that matches the style representation of the original image. We do so by minimizing the mean squared distance between the feature correlation map of the style image and the input image. The contribution of each layer to the total style loss is described by where Gˡᵢⱼ and Aˡᵢⱼ are the respective style representation in layer l of input image x and style image a. Nl describes the number of feature maps, each of size Ml=height∗width. 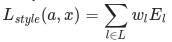Thus, the total style loss across each layer is where we weight the contribution of each layer’s loss by some factor wl. 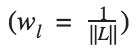In our case, we weight each layer equally: This is implemented simply:

def gram_matrix(input_tensor):
  # We make the image channels first 
  channels = int(input_tensor.shape[-1])
  a = tf.reshape(input_tensor, [-1, channels])
  n = tf.shape(a)[0]
  gram = tf.matmul(a, a, transpose_a=True)
  return gram / tf.cast(n, tf.float32)
 
def get_style_loss(base_style, gram_target):
  """Expects two images of dimension h, w, c"""
  # height, width, num filters of each layer
  height, width, channels = base_style.get_shape().as_list()
  gram_style = gram_matrix(base_style)
  
  return tf.reduce_mean(tf.square(gram_style - gram_target))

Run Gradient Descent

If you aren’t familiar with gradient descent/backpropagation or need a refresher, you should definitely check out this resource. In this case, we use the Adam optimizer in order to minimize our loss. We iteratively update our output image such that it minimizes our loss: we don’t update the weights associated with our network, but instead we train our input image to minimize loss. In order to do this, we must know how we calculate our loss and gradients. Note that the L-BFGS optimizer, which if you are familiar with this algorithm is recommended, but isn’t used in this tutorial because a primary motivation behind this tutorial was to illustrate best practices with eager execution. By using Adam, we can demonstrate the autograd/gradient tape functionality with custom training loops.

Compute the loss and gradients

We’ll define a little helper function that will load our content and style image, feed them forward through our network, which will then output the content and style feature representations from our model.

def get_feature_representations(model, content_path, style_path):
  """Helper function to compute our content and style feature representations.
 
  This function will simply load and preprocess both the content and style 
  images from their path. Then it will feed them through the network to obtain
  the outputs of the intermediate layers. 
  
  Arguments:
    model: The model that we are using.
    content_path: The path to the content image.
    style_path: The path to the style image
    
  Returns:
    returns the style features and the content features. 
  """
  # Load our images in 
  content_image = load_and_process_img(content_path)
  style_image = load_and_process_img(style_path)
  
  # batch compute content and style features
  stack_images = np.concatenate([style_image, content_image], axis=0)
  model_outputs = model(stack_images)
  
  # Get the style and content feature representations from our model  
  style_features = [style_layer[0] for style_layer in model_outputs[:num_style_layers]]
  content_features = [content_layer[1] for content_layer in model_outputs[num_style_layers:]]
  return style_features, content_features

Here we use tf.GradientTape to compute the gradient. It allows us to take advantage of the automatic differentiation available by tracing operations for computing the gradient later. It records the operations during the forward pass and then is able to compute the gradient of our loss function with respect to our input image for the backwards pass.

def compute_loss(model, loss_weights, init_image, gram_style_features, content_features):
  """This function will compute the loss total loss.
  
  Arguments:
    model: The model that will give us access to the intermediate layers
    loss_weights: The weights of each contribution of each loss function. 
      (style weight, content weight, and total variation weight)
    init_image: Our initial base image. This image is what we are updating with 
      our optimization process. We apply the gradients wrt the loss we are 
      calculating to this image.
    gram_style_features: Precomputed gram matrices corresponding to the 
      defined style layers of interest.
    content_features: Precomputed outputs from defined content layers of 
      interest.
      
  Returns:
    returns the total loss, style loss, content loss, and total variational loss
  """
  style_weight, content_weight, total_variation_weight = loss_weights
  
  # Feed our init image through our model. This will give us the content and 
  # style representations at our desired layers. Since we're using eager
  # our model is callable just like any other function!
  model_outputs = model(init_image)
  
  style_output_features = model_outputs[:num_style_layers]
  content_output_features = model_outputs[num_style_layers:]
  
  style_score = 0
  content_score = 0

  # Accumulate style losses from all layers
  # Here, we equally weight each contribution of each loss layer
  weight_per_style_layer = 1.0 / float(num_style_layers)
  for target_style, comb_style in zip(gram_style_features, style_output_features):
    style_score += weight_per_style_layer * get_style_loss(comb_style[0], target_style)
    
  # Accumulate content losses from all layers 
  weight_per_content_layer = 1.0 / float(num_content_layers)
  for target_content, comb_content in zip(content_features, content_output_features):
    content_score += weight_per_content_layer* get_content_loss(comb_content[0], target_content)
  
  style_score *= style_weight
  content_score *= content_weight
  total_variation_score = total_variation_weight * total_variation_loss(init_image)

  # Get total loss
  loss = style_score + content_score + total_variation_score 
  return loss, style_score, content_score, total_variation_score

Then computing the gradients is easy:

def compute_grads(cfg):
  with tf.GradientTape() as tape: 
    all_loss = compute_loss(**cfg)
  # Compute gradients wrt input image
  total_loss = all_loss[0]
  return tape.gradient(total_loss, cfg['init_image']), all_loss

Apply and run the style transfer process

And to actually perform the style transfer:

def run_style_transfer(content_path, 
                       style_path,
                       num_iterations=1000,
                       content_weight=1e3, 
                       style_weight = 1e-2): 
  display_num = 100
  # We don't need to (or want to) train any layers of our model, so we set their trainability
  # to false. 
  model = get_model() 
  for layer in model.layers:
    layer.trainable = False
  
  # Get the style and content feature representations (from our specified intermediate layers) 
  style_features, content_features = get_feature_representations(model, content_path, style_path)
  gram_style_features = [gram_matrix(style_feature) for style_feature in style_features]
  
  # Set initial image
  init_image = load_and_process_img(content_path)
  init_image = tfe.Variable(init_image, dtype=tf.float32)
  # Create our optimizer
  opt = tf.train.AdamOptimizer(learning_rate=10.0)

  # For displaying intermediate images 
  iter_count = 1
  
  # Store our best result
  best_loss, best_img = float('inf'), None
  
  # Create a nice config 
  loss_weights = (style_weight, content_weight)
  cfg = {
      'model': model,
      'loss_weights': loss_weights,
      'init_image': init_image,
      'gram_style_features': gram_style_features,
      'content_features': content_features
  }
    
  # For displaying
  plt.figure(figsize=(15, 15))
  num_rows = (num_iterations / display_num) // 5
  start_time = time.time()
  global_start = time.time()
  
  norm_means = np.array([103.939, 116.779, 123.68])
  min_vals = -norm_means
  max_vals = 255 - norm_means   
  for i in range(num_iterations):
    grads, all_loss = compute_grads(cfg)
    loss, style_score, content_score = all_loss
    # grads, _ = tf.clip_by_global_norm(grads, 5.0)
    opt.apply_gradients([(grads, init_image)])
    clipped = tf.clip_by_value(init_image, min_vals, max_vals)
    init_image.assign(clipped)
    end_time = time.time() 
    
    if loss < best_loss:
      # Update best loss and best image from total loss. 
      best_loss = loss
      best_img = init_image.numpy()

    if i % display_num == 0:
      print('Iteration: {}'.format(i))        
      print('Total loss: {:.4e}, ' 
            'style loss: {:.4e}, '
            'content loss: {:.4e}, '
            'time: {:.4f}s'.format(loss, style_score, content_score, time.time() - start_time))
      start_time = time.time()
      
      # Display intermediate images
      if iter_count > num_rows * 5: continue 
      plt.subplot(num_rows, 5, iter_count)
      # Use the .numpy() method to get the concrete numpy array
      plot_img = init_image.numpy()
      plot_img = deprocess_img(plot_img)
      plt.imshow(plot_img)
      plt.title('Iteration {}'.format(i + 1))

      iter_count += 1
  print('Total time: {:.4f}s'.format(time.time() - global_start))
      
  return best_img, best_loss 

And that’s it!

Let’s run it on our image of the turtle and Hokusai’s The Great Wave off Kanagawa:

best, best_loss = run_style_transfer(content_path, 
                                     style_path,
                                     verbose=True,
                                     show_intermediates=True)

Image of Green Sea Turtle by P.Lindgren [CC BY-SA 3.0 (https://creativecommons.org/licenses/by-sa/3.0)], from Wikimedia Common

Watch the iterative process over time: Here are some other cool examples of what neural style transfer can do. Check it out!

Image of Tuebingen — Photo By: Andreas Praefcke [GFDL (http://www.gnu.org/copyleft/fdl.html) or CC BY 3.0 (https://creativecommons.org/licenses/by/3.0)], from Wikimedia Commons and Image of Starry Night by Vincent van Gogh, Public domain

Image of Tuebingen — Photo By: Andreas Praefcke [GFDL (http://www.gnu.org/copyleft/fdl.html) or CC BY 3.0 (https://creativecommons.org/licenses/by/3.0)], from Wikimedia Commons and Image of Composition 7 by Vassily Kandinsky, Public Domain

Image of Tuebingen — Photo By: Andreas Praefcke [GFDL (http://www.gnu.org/copyleft/fdl.html) or CC BY 3.0 (https://creativecommons.org/licenses/by/3.0)], from Wikimedia Commons and Image of Pillars of Creation by NASA, ESA, and the Hubble Heritage Team, Public Domain

Try out your own images!

Key Takeaways

What we covered:

• We built several different loss functions and used backpropagation to transform our input image in order to minimize these losses.
  
• In order to do this, we loaded in a pretrained model and used its learned feature maps to describe the content and style representation of our images.
  
• Our main loss functions were primarily computing the distance in terms of these different representations.
  
• We implemented this with a custom model and eager execution.
  
• We built our custom model with the Functional API.
  
• Eager execution allows us to dynamically work with tensors, using a natural python control flow.
  
• We manipulated tensors directly, which makes debugging and working with tensors easier.
  

We iteratively updated our image by applying our optimizers update rules using tf.gradient. The optimizer minimized the given losses with respect to our input image.