ožujka 12, 2019 —
Posted by Pavel Sountsov, Chris Suter, Jacob Burnim, Joshua V. Dillon, and the TensorFlow Probability team
BackgroundAt the 2019 TensorFlow Dev Summit, we announced Probabilistic Layers in TensorFlow Probability (TFP). Here, we demonstrate in more detail how to use TFP layers to manage the uncertainty inherent in regression predictions.
Regression and ProbabilityRegression is one of the most basic …

negloglik = lambda y, p_y: -p_y.log_prob(y)import tensorflow as tf
import tensorflow_probability as tfp
tfd = tfp.distributions
# Build model.
model = tf.keras.Sequential([
tf.keras.layers.Dense(1),
tfp.layers.DistributionLambda(lambda t: tfd.Normal(loc=t, scale=1)),
])
# Do inference.
model.compile(optimizer=tf.optimizers.Adam(learning_rate=0.05), loss=negloglik)
model.fit(x, y, epochs=500, verbose=False)
# Make predictions.
yhat = model(x_tst)tfp.layers.DistributionLambda layer in fact returns a special instance of tfd.Distribution (see Appendix A for more details about this), so we are free to take its mean and plot it next to the data:mean = yhat.mean()
# Build model.
model = tfk.Sequential([
tf.keras.layers.Dense(1 + 1),
tfp.layers.DistributionLambda(
lambda t: tfd.Normal(loc=t[..., :1],
scale=1e-3 + tf.math.softplus(0.05 * t[..., 1:]))),
])
# Do inference.
model.compile(optimizer=tf.optimizers.Adam(learning_rate=0.05), loss=negloglik)
model.fit(x, y, epochs=500, verbose=False)
# Make predictions.
yhat = model(x_tst)mean = yhat.mean()
stddev = yhat.stddev()
mean_plus_2_stddev = mean - 2. * stddev
mean_minus_2_stddev = mean + 2. * stddev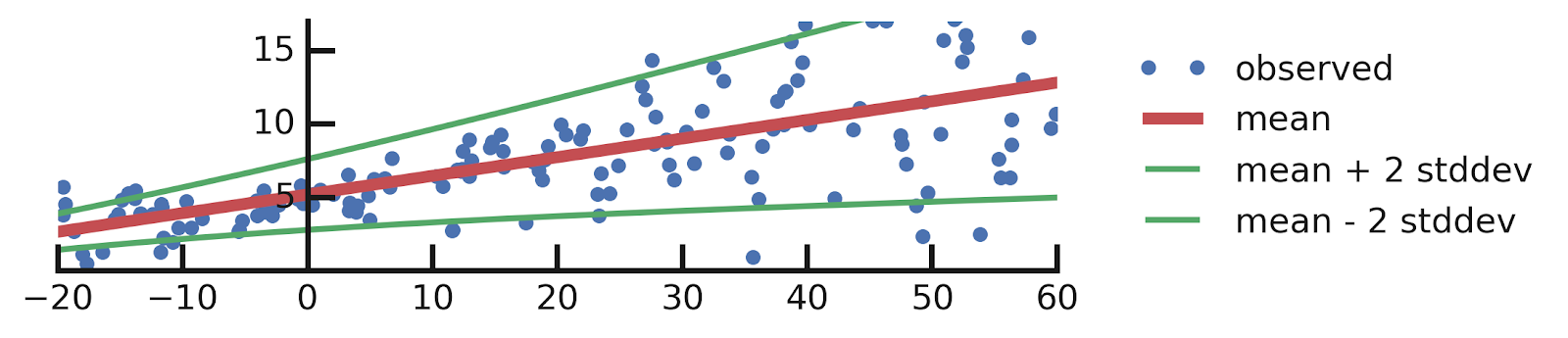
Dense layer with TFP’s DenseVariational layer.DenseVariational layer uses a variational posterior Q(w) over the weights to represent the uncertainty in their values. This layer regularizes Q(w) to be close to the prior distribution P(w), which models the uncertainty in the weights before we look into the data.# Build model.
model = tf.keras.Sequential([
tfp.layers.DenseVariational(1, posterior_mean_field, prior_trainable),
tfp.layers.DistributionLambda(lambda t: tfd.Normal(loc=t, scale=1)),
])
# Do inference.
model.compile(optimizer=tf.optimizers.Adam(learning_rate=0.05), loss=negloglik)
model.fit(x, y, epochs=500, verbose=False)
# Make predictions.
yhats = [model(x_tst) for i in range(100)]DenseVariational layer is simple. One interesting aspect of the code above is that when we make predictions using a model with such a layer, we get a different answer every time we do so. This is because DenseVariational essentially defines an ensemble of models. Let us see what this ensemble tells us about the parameters of our model.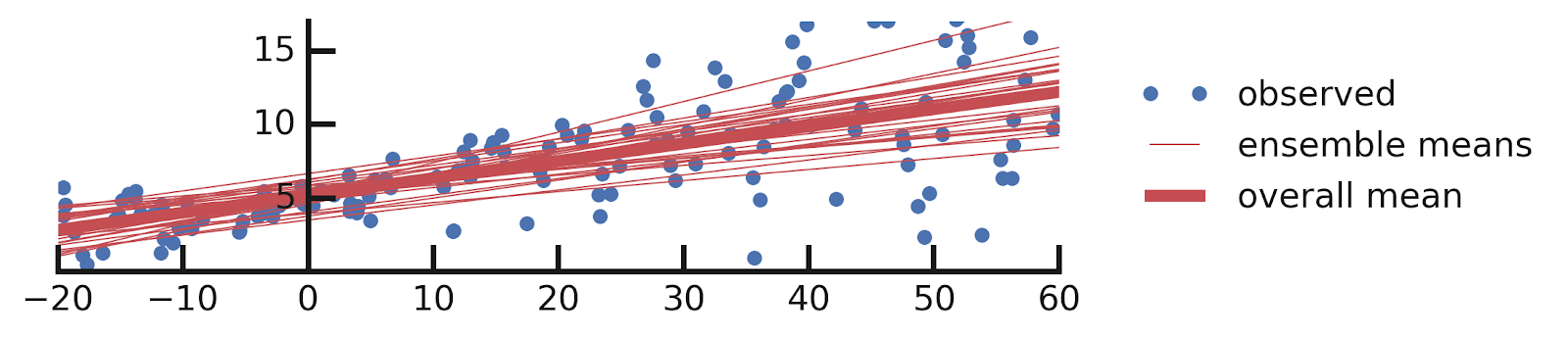
# Build model.
model = tf.keras.Sequential([
tfp.layers.DenseVariational(1 + 1, posterior_mean_field, prior_trainable),
tfp.layers.DistributionLambda(
lambda t: tfd.Normal(loc=t[..., :1],
scale=1e-3 + tf.math.softplus(0.01 * t[..., 1:]))),
])
# Do inference.
model.compile(optimizer=tf.optimizers.Adam(learning_rate=0.05), loss=negloglik)
model.fit(x, y, epochs=500, verbose=False);
# Make predictions.
yhats = [model(x_tst) for _ in range(100)]DenseVariational layer to also model the scale of the label distribution. As in our previous solution, we get an ensemble of models, but this time they all also report the variability of y as a function of x. Let us plot this ensemble:
negloglik function that implements the negative log-likelihood, while making local alterations to the model to handle more and more types of uncertainty. The API also lets you freely switch between Maximum Likelihood learning, Type-II Maximum Likelihood and and a full Bayesian treatment. We believe that this API significantly simplifies construction of probabilistic models and are excited to share it with the world.VariationalGaussianProcess layer, which uses a variational approximation (similar in spirit to what we did in case 3 and 4 above) to a full Gaussian Process for an efficient yet flexible regression model. For simplicity, we’ll be considering only the epistemic uncertainty about the form of the relationship between inputs and labels. In terms of the assumptions we’ll be making, we’ll simply assume that the function we’re fitting is locally smooth: it can vary as much as it wants across the entire dataset, but if two inputs are close, it’ll return similar values.num_inducing_points = 40
model = tf.keras.Sequential([
tf.keras.layers.InputLayer(input_shape=[1], dtype=x.dtype),
tf.keras.layers.Dense(1, kernel_initializer='ones', use_bias=False),
tfp.layers.VariationalGaussianProcess(
num_inducing_points=num_inducing_points,
kernel_provider=RBFKernelFn(dtype=x.dtype),
event_shape=[1],
inducing_index_points_initializer=tf.constant_initializer(
np.linspace(*x_range, num=num_inducing_points,
dtype=x.dtype)[..., np.newaxis]),
unconstrained_observation_noise_variance_initializer=(
tf.constant_initializer(
np.log(np.expm1(1.)).astype(x.dtype))),
),
])
# Do inference.
batch_size = 32
loss = lambda y, rv_y: rv_y.variational_loss(
y, kl_weight=np.array(batch_size, x.dtype) / x.shape[0])
model.compile(optimizer=tf.optimizers.Adam(learning_rate=0.01), loss=loss)
model.fit(x, y, batch_size=batch_size, epochs=1000, verbose=False)
# Make predictions.
yhats = [model(x_tst) for _ in range(100)]
DistributionLambda is a special Keras layer that uses a Python lambda to construct a distribution conditioned on the layer inputs:layer = tfp.layers.DistributionLambda(lambda t: tfd.Normal(t, 1.))
distribution = layer(2.)
assert isinstance(distribution, tfd.Normal)
distribution.loc
# ==> 2.
distribution.stddev()
# ==> 1.negloglik loss function as we did, because Keras passes the output of the final layer of the model into the loss function, and for the models in this post, all those layers return distributions. See the Variational Autoencoders with Tensorflow Probability Layers post for more ways to use these layers.DenseVariational layer enables learning a distribution over its weights using variational inference. This is done by maximizing the ELBO (Evidence Lower BOund) objective:
DenseVariational computes the two terms of the ELBO separately. The first term is computed by approximating it with a single random sample from Q. If we look at that term closely, then for any specific value of w it is exactly the negative log-likelihood loss we’ve been using for regression in this post. Thus, by simply drawing a random set of weights from Q and then computing the regular loss, we automatically approximate the first term of ELBO.def prior_trainable(kernel_size, bias_size=0, dtype=None):
n = kernel_size + bias_size
return tf.keras.Sequential([
tfp.layers.VariableLayer(n, dtype=dtype),
tfp.layers.DistributionLambda(lambda t: tfd.Independent(
tfd.Normal(loc=t, scale=1),
reinterpreted_batch_ndims=1)),
])DistributionLambda layer! The only new component here is the VariableLayer which simply returns the value of a trainable variable, ignoring any inputs (because the prior is not conditioned on any inputs). Note that if we wanted to convert this to a non-trainable prior, we would pass trainable=False to VariableLayer constructor.


ožujka 12, 2019
—
Posted by Pavel Sountsov, Chris Suter, Jacob Burnim, Joshua V. Dillon, and the TensorFlow Probability team
BackgroundAt the 2019 TensorFlow Dev Summit, we announced Probabilistic Layers in TensorFlow Probability (TFP). Here, we demonstrate in more detail how to use TFP layers to manage the uncertainty inherent in regression predictions.
Regression and ProbabilityRegression is one of the most basic …